First-order reversal curves are a powerful tool yielding microscopic information without the need for micron sized lateral resolution. The concept itself is simple and a measurement can in principle be conducted with any magnetometer capable of measuring a hysteresis loop. However, finishing a measurement, its evaluation, and interpretation within a convenient time frame can turn out to be challenging. Moreover, FORC diagrams can be quite challenging to interpret properly. In literature FORC are often seen as a characteristic magnetic fingerprint of a material, simply because the results can in fact be quite difficult to interpret. Nevertheless, FORC has proven to be an indispensable tool for magnetic characterization.
|
|
|
 |
Measurement of FORC diagrams with MOKEFast high resolution first-order reversal curve measurements yield a unique insight into magnetization reversal processes. |
|
|
|
 |
GPU accelerated evaluation of FORC diagrams - gFORCThe GPU accelerated first-order reversal-curve calculator (gFORC) is not only 1000x faster than conventional approaches but also provides the user with some valuable information about the optimum smoothing factor. |
|
|
|
 |
Interpretation of FORC diagramsFORC diagrams beyond the so-called Preisach model are difficult to interpret. We leverage a combination of microstructure design and microscopic imaging to push the boundaries of the theoretical framework of FORC. |
|
|
|
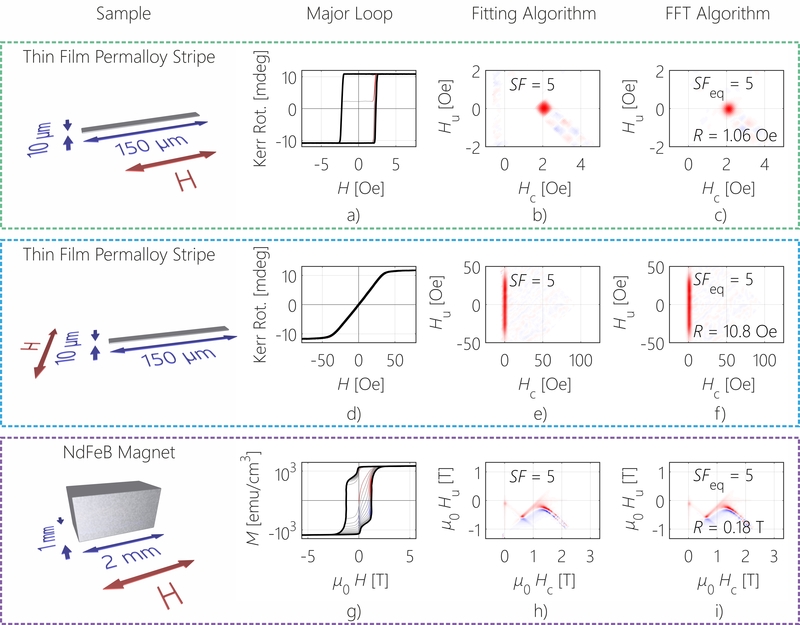
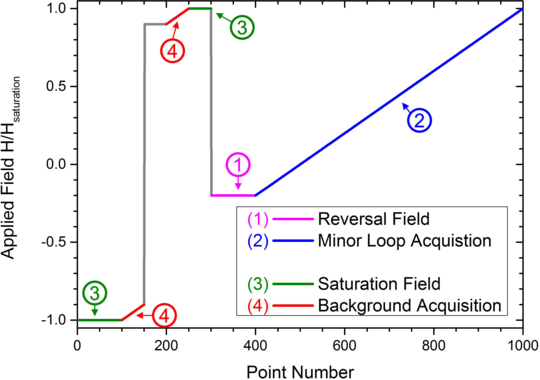
Fast high resolution first-order reversal curve measurements yield a unique insight into magnetization reversal processes. To acquire a FORC distribution a large number of minor hysteresis loops is measured. This allows the separation of irreversible magnetization processes by their respective coercive and interaction fields. Thereby, enabling the interpretation of complex magnetization reversal mechanisms with multiple steps. Magneto-optical Kerr effect measurements have been adapted for fast measurements, allowing 1000x faster measurements compared to conventional methods. This opens up the possibility of parametric investigations of a large variety of systems, e.g. magnetic antidote lattices, hard magnets, or superconductor heterostructures.

Field profile for fast acquisition of minor hysteresis loops by magneto-optical Kerr effect measurements. From: J. Gräfe et al. Review of Scientific Instruments 85, 023901 (2014). [ ]
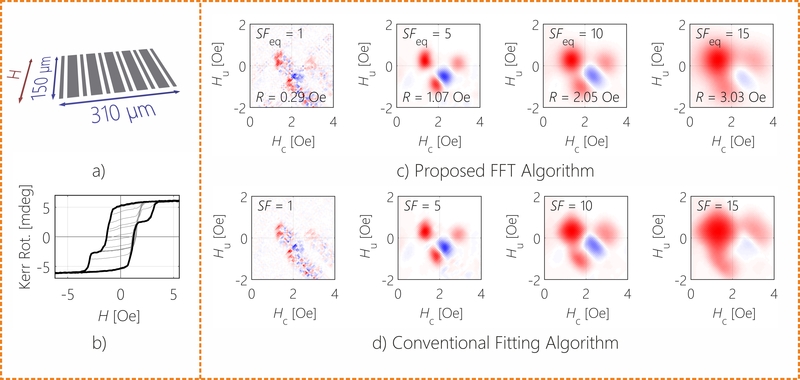
While the acquisition of first-order reversal curves (FORCs) can be accelerated drastically by utilizing the magneto-optical Kerr-effect, the most commonly used processing algorithm is approximately 20 years old and hence, provides room for additional optimizations with today’s technology. The GPU accelerated first-order reversal-curve calculator (gFORC) is not only 1000x faster than conventional approaches but also provides the user with some valuable information about the optimum smoothing factor, which is a measure for how much a FORC diagram is smoothed before processing. Although the gFORC algorithm uses a new Fourier approach results compare well to results obtained by the conventional algorithm. This makes it user friendly for veterans as well as newcomers in the field of FORC.

Comparison between the conventional and the FFT algorithm. From: F. Groß et al., Journal of Applied Physics 126, 163901 (2019). [ ]
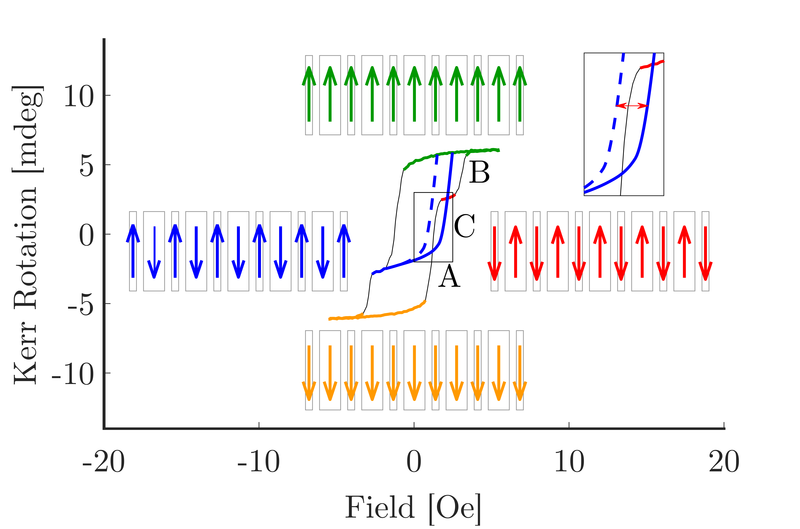
First-order reversal curves (FORCs) are a powerful tool to investigate magnetic materials without the need for micro-sized magnetic resolution. However, the measurement output, a so-called FORC density, is not always straightforward to interpret, especially in the presence of micromagnetic interactions between magnetic components. This is why FORCs are often interpreted as a magnetic fingerprint instead of a measurement method yielding quantitative information about a system. Hence, a deeper understanding of FORC is necessary to reliably interpret FORC diagrams and all of their features since they, although hard to interpret, do in fact contain valuable information about the magnetic interactions within the system.
Micromagnetic explanation for additional features in a FORC diagram. From: F. Groß et al., Physical Review B 99, 064401 (2019). [ ]
