gFORC: A graphics processing unit accelerated first-order reversal-curve calculator
2019
Article
mms
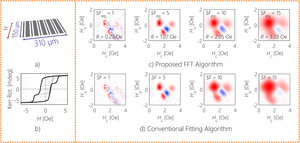
First-order reversal-curves have proven to be an indispensable characterization tool for physics as well as for geology. However, the conventional evaluation algorithm requires a lot of computational effort for a comparable easy task to overcome measurement noise. In this work, we present a new evaluation approach, which exploits the diversity of Fourier space to not only speed up the calculation by a factor of 1000 but also move away from the conventional smoothing factor toward real field resolution. By comparing the baseline resolution of the new and the old algorithm, we are able to deduce an analytical equation that converts the smoothing factor into field resolution, making the old and new algorithm comparable. We find excellent agreement not only for various systems of increasing complexity but also over a large range of smoothing factors. The achieved speedup enables us to calculate a large number of first-order reversal-curve diagrams with increasing smoothing factor allowing for an autocorrelation approach to find a hard criterion for the optimum smoothing factor. This previously computational prohibitive evaluation of first-order reversal-curves solves the problem of over- and undersmoothing by increasing general readability and preventing information destruction.
| Author(s): | Groß, F. and Martínez-García, J. C. and Ilse, S. E. and Schütz, G. and Goering, E. and Rivas, M. and Gräfe, J. |
| Journal: | {Journal of Applied Physics} |
| Volume: | 126 |
| Number (issue): | 16 |
| Year: | 2019 |
| Publisher: | AIP Publishing |
| Department(s): | Modern Magnetic Systems |
| Research Project(s): |
First-Order Reversal Curves
|
| Bibtex Type: | Article (article) |
| Address: | New York, NY |
| DOI: | 10.1063/1.5120495 |
| Language: | eng |
|
BibTex @article{escidoc:3171857,
title = {{gFORC: A graphics processing unit accelerated first-order reversal-curve calculator}},
author = {Gro\ss, F. and Mart\'{i}nez-Garc\'{i}a, J. C. and Ilse, S. E. and Sch\"utz, G. and Goering, E. and Rivas, M. and Gr\"afe, J.},
journal = {{Journal of Applied Physics}},
volume = {126},
number = {16},
publisher = {AIP Publishing},
address = {New York, NY},
year = {2019},
doi = {10.1063/1.5120495}
}
|
|